Applications de la théorie ergodique aux fractions continues

|

|
| F. Heuwelyckx | S. Scolas |
Nous avons réalisé ce projet parce qu'il nous permettait d'utiliser une notion probabiliste (théorie ergodique) dans le cadre de la théorie des nombres. Le plus intéressant c'est la manière dont on réécrivait les nombres réels et les propriétés et applications originales qui en découlaient.
L'écriture d'un nombre réel \(x\) en fraction continue consiste juste à trouver un nombre entier \(a_0\) et des nombres naturels non nuls \(a_1, a_2,...\) tels que l'égalité suivante soit vraie: \[ x=a_0 + \frac{1}{a_1+\frac{1}{a_2+\frac{1}{\dots}}}. \] Une transformation connue permet de trouver les valeurs des \(a_i\). Cette manière de voir les nombres permet d'approcher n'importe quel nombre par des fractions de plus en plus précises. C'est grâce à cette méthode par exemple que l'on peut déduire qu'une bonne estimation du célèbre nombre \(\pi\) est \(22/7\) car \[ \pi=3 + \frac{1}{7+\frac{1}{15+\frac{1}{\dots}}}. \] En s'arrêtant à la première étape, on déduit que \(\pi\approx 3+1/7=22/7\). Certains nombres célèbres ont une plus belle écriture en fractions continues qu'en base décimale. Si on prend \(\sqrt{2}\approx1{,}414213562\), ce nombre s'écrit simplement en fractions continues: \(a_0=1\) tandis que les \(a_1, a_2, \dots\) ont tous la valeur 2. Le mathématicien Christiaan Huygens utilisa les fractions continues au XVIIe siècle afin d'élaborer son automate planétaire. Il lui fallait déterminer le nombre de dents qu'auraient les roues de son appareil. Le nombre de dents nécessaires pour le fabriquer était malheureusement trop important. Il lui était donc impossible de construire un automate parfait. Les fractions continues lui ont permis de construire un appareil dont l'erreur par siècle n'était que de quarante secondes.
La théorie ergodique définit des propriétés vérifiées pour des transformations particulières. Les résultats de l'application de cette théorie sur les réels offrent une curiosité étonnante : la fréquence d'apparition des nombres dans l'écriture ! Si on choisit un réel complètement au hasard et que l'on regarde son écriture en base décimale, chacun des chiffres a une chance sur dix d'apparaître. Ce n'est absolument pas le cas des \(a_1,a_2,\dots\) dans notre nouvelle écriture ! Premièrement, leurs valeurs ne sont pas limitées aux seuls chiffres 0 à 9 mais à n'importe quel nombre naturel. Ensuite, chacun des nombres n'a pas la même chance d'être observé: le nombre 1 vient dans 41% des cas alors que le nombre 10 est beaucoup plus rare ; seulement une fois sur cent! Nous avons démontré ce résultat grâce à la théorie probabiliste. Mais ce n'est qu'un petit exemple de l'intérêt qu'a pu nous apporter cet approfondissement...
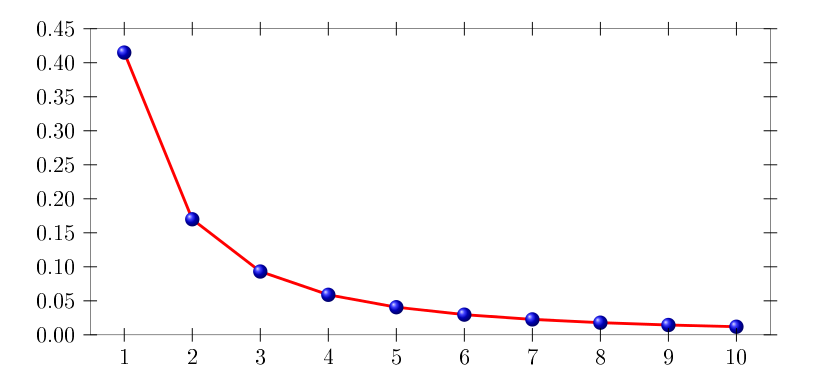
Fréquence des différents coefficients.